Sri Yantra lépésről lépésre rajzolás AutoCAD-ben

Olvasói vélemények

Jelenleg nincsenek olvasói vélemények. Az értékelés 2 olvasói szavazat alapján történt.

Eredeti címe:

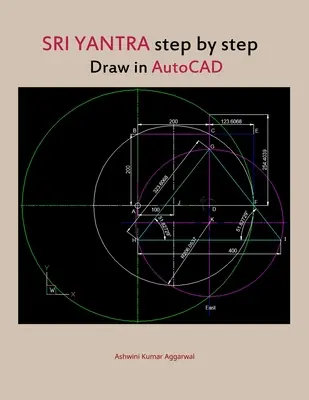
Sri Yantra step by step draw in AutoCAD

Könyv tartalma:

A pontossággal és precizitással tervezett Sri Yantra értékes, gyönyörű és rendkívül jóindulatú. A rajzolás megkezdéséhez használjon egy 2D rajzoló mérnöki szoftvert, pl. AutoCAD, BricsCAD, nanoCAD, LibreCAD stb.

⬤  Állítsa be a Méretek pontosságát négytizedes helyre, pl. 0. 0000

⬤ Minden egyes megrajzolt vonal, szög vagy kör esetén vegye a Dimenziót, és nézze meg, hogy pontosan egyezik-e.

⬤ Még egy csekély hiba is elveszíti a Sri Yantra szépségét és értékét.

⬤ 1 Négyzet ABCD, 200 oldal.

⬤ 2 A négyzetet a J-nél felezzük fel.

⬤ Készítsünk JCD derékszögű háromszöget JC = 223 hipotenuzával. 6068, szög CJD = 63. 4349.

⬤ 3 Rajzoljunk fekete kört középpontja J, sugara = hipotenúzája JC = 223. 6068.

⬤ 4 Hosszabbítsuk meg az ABCD négyzetet ABEF négyszöggé, amelynek hosszabbik oldala AF = BE = 323. 6068.

⬤ 5 Rajzoljunk zöld kört középpontja A, sugara = 323. 6068.

⬤ 6 Hosszabbítsuk meg a DC négyzet oldalát úgy, hogy a g felső pontnál érintse a zöld kört. A Dg hossza = 254. 4039.

⬤ A pontosság kedvéért.

⬤ Hosszabbítsuk meg a CD négyzet oldalát, hogy az alsó ponton érintse a zöld kört. Ez a hossz = 254. 4039.

⬤ Ezeknek a két hossznak egyenlőnek kell lennie. Ez csak azért van, hogy ellenőrizzük, jól haladunk-e eddig.

⬤ Ha mindkét hossz Egyenlő, akkor megtaláltuk a T1u háromszög g csúcsát.

⬤ 7 Most csatlakoztassuk A-t g-hez, és megkapjuk a T1u aranymetszés-háromszög oldalát.

⬤ Megjegyezzük, hogy Oldal Ag = a zöld kör sugara = 323. 6068.

⬤ 8 Másoljuk és tükrözzük az Ag oldalt, hogy megkapjuk az aranymetszéses háromszög gi oldalát.

⬤ 9 Egyesítsük az A és i pontokat, hogy megkapjuk a T1u aranymetszés-háromszög Ai alapját.

Aranymetszetű háromszögT1u A legnagyobb felfelé mutató csúcsú háromszög a Sri Yantra kezdő pontja.

⬤ Az Aranymetszetű háromszög T1u = Agi méretei pontosan kell, hogy legyenek.

⬤ Az alapvonal hossza = 400.

⬤ Az egyenlő szárú oldalak hossza = 323. 6068.

⬤ Egyenként egyenlő szárú szög = 51. 82729.